자바 알고리즘 문제 풀이 입문. ch07. Recursive, Tree, Graph(DFS, BFS 기초) : 이진 트리 순회

 

https://hyejin.tistory.com/1256

자바 알고리즘 문제 풀이 입문. ch07. Recursive, Tree, Graph(DFS, BFS 기초) : 피보나치 재귀 (메모이제이

-> 이전 문제 풀이 

 

 

5. 이진 트리 순회 

설명

아래 그림과 같은 이진트리를 전위순회와 후위순회를 연습해보세요.

 

 

 

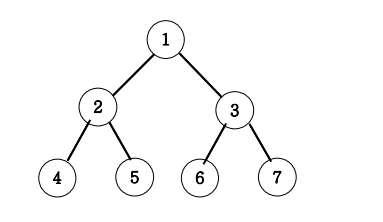
전위순위 출력 

 1 2 4 5 3 6 7

 

 

중위순위 출력 

 4 2 5 1 6 3 7

 

 

후위순위 출력 

 4 5 2 6 7 3 1

 

 

문제 풀이

public class BinaryTreeTraversal
{
   Node root;
   
   public void DFS(Node root)
   {
      if (root == null) { // 말단까지 갔다는 얘기
         return;
      }else {
         System.out.print(root.data + " "); // 전위 순회
         DFS(root.lt);
//       System.out.print(root.data + " "); // 중위 순회
         DFS(root.rt);
//       System.out.print(root.data + " "); // 후위 순회
      }
   
   }
   public static void main(String[] args)
   {
      BinaryTreeTraversal tree = new BinaryTreeTraversal();
      tree.root = new Node(1);
      tree.root.lt = new Node(2);
      tree.root.rt = new Node(3);
      tree.root.lt.lt = new Node(4);
      tree.root.lt.rt = new Node(5);
      tree.root.rt.lt = new Node(6);
      tree.root.rt.rt = new Node(7);
      tree.DFS(tree.root);
      
   }
}

class Node {
   int data;
   Node lt, rt;
   
   public Node(int val)
   {
      data = val;
      lt = rt = null;
   }
}

👾 : 트리 관련 문제는 풀어본 적이 없어서 이번엔 강의를 먼저 들어봤다. 

 

class Node {
   int data;
   Node lt, rt;
   
   public Node(int val)
   {
      data = val;
      lt = rt = null;
   }
}

우선 Node라는 클래스를 하나 만들고, 그 다음 data 가 부모 노드, lt 자는 왼쪽 자식, rt는 오른쪽 자식을 설정할 것이다. 

생성자에는 val 를 받으면 우선 부모 노드의 data에 그 값을 넣어두고, lt와 rt에는 null 값을 넣어준다. 

 

BinaryTreeTraversal 클래스를 만들고, 거기에 전역 변수로 Node 변수를 하나 선언했다. 

 

public static void main(String[] args)
{
   BinaryTreeTraversal tree = new BinaryTreeTraversal();
   tree.root = new Node(1);
   tree.root.lt = new Node(2);
   tree.root.rt = new Node(3);
   tree.root.lt.lt = new Node(4);
   tree.root.lt.rt = new Node(5);
   tree.root.rt.lt = new Node(6);
   tree.root.rt.rt = new Node(7);
   tree.DFS(tree.root);
   
}

그 다음 tree.root에 Node 객체 하나를 생성해서 값을 1로 설정해준다. (제일 최상위 노드) 

그리고 이 1의 노드에서 lt 에는 왼쪽 값 Node 2를 생성해주고, 오른쪽 rt 값에는 Node 3을 생성해준다. 

그리고 이어서 Node2의 왼쪽 lt 값에는 Node 4를 생성해주고, 오른쪽 rt 값에는 Node 5을 생성해준다. 

그리고 다음 Node3의 왼쪽 lt 값에는 Node6을 생성해주고, 오른쪽 rt 값에는 Node 7 을 생성해준다. 

 

-> 이렇게 하면 그림이 이런식으로 그려질 것이다. (그림은 강의에서 캡쳐했음..) 

그리고 Node4, 5, 6, 7 에서는 null 값이 들어갈 것이고 이러면 말단 데이터라는 것이다. 

 

 

    public void DFS(Node root)
   {
      if (root == null) { // 말단까지 갔다는 얘기
         return;
      }else {
         System.out.print(root.data + " "); // 전위 순회
         DFS(root.lt);
//       System.out.print(root.data + " "); // 중위 순회
         DFS(root.rt);
//       System.out.print(root.data + " "); // 후위 순회
      }
   
   }

DFS 함수인데 이때 root 가 null 이라는 건 이제 자식 노드 끝까지 갔단 얘기 이므로 return 할 때 아무것도 넘겨주지 않고 끝난다. 

그리고 null 이 아니라면 이제 재귀 함수를 호출 할 것인데 이번에는 재귀 함수를 두번 호출해야 한다. 

DFS(root.lt) 와 DFS(root.rt) 를 호출하면 되고, 이때 출력을 어디서 하느냐에 따라 전위, 중위, 후위 출력을 할 수 있다. 

 

 

    public void DFS(Node root)
   {
      if (root == null) { // 말단까지 갔다는 얘기
         return;
      }else {
         System.out.print(root.data + " "); // 전위 순회
         DFS(root.lt);
         DFS(root.rt);
      }
   
   }

 

-> 맨 위에서 출력하면 먼저 root.data를 출력하고 DFS(root.lt)와 DFS(root.rt)를 출력한다. 

그렇기 때문에 전위 순위로 출력을 할 수 있다. 

1 2 4 5 3 6 7 

 

 

    public void DFS(Node root)
   {
      if (root == null) { // 말단까지 갔다는 얘기
         return;
      }else {
         DFS(root.lt);
         System.out.print(root.data + " "); // 중위 순회
         DFS(root.rt);
      }
   
   }

-> DFS(root.lt)와 DFS(root.rt) 사이에 출력 코드가 위치하면 lt 출력하고, root.data 출력하고, rt를 출력하기 때문에 

중위 순위로 출력할 수 있다. 

4 2 5 1 6 3 7

 

 

    public void DFS(Node root)
   {
      if (root == null) { // 말단까지 갔다는 얘기
         return;
      }else {
         DFS(root.lt);
         DFS(root.rt);
         System.out.print(root.data + " "); // 후위 순회
      }
   
   }

 

-> 마지막으로 출력 코드가 가장 마지막에 위치하면 DFS(root.lt)와 DFS(root.rt) 모두 출력한 후에 root.data 를 출력하기 때문에 후위 순위로 출력할 수 있다. 

4 5 2 6 7 3 1